1.3 Vector Equations
- vectors in R^n: algebraic properties
R n 스페이스에서 벡터를 표현하는 R은 실수 공간을 의미하며 n은 양의 정수이다.
실수 공간에서의 몇 차원 공간인지를 의미한다.
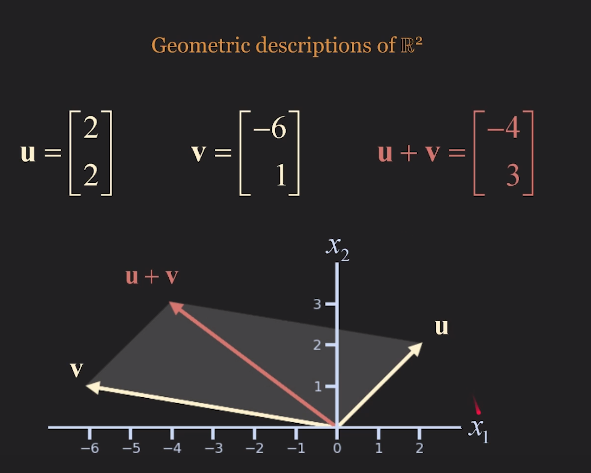
아래 그림처럼 백터는 주로 열 백터로 표현한다.

Scalar multiplication
c=5 // scalar
u = [[3], [-1]]
(3,-1)
cu =5[[3], [-1]] = [[5*3], [5*(-1)]]
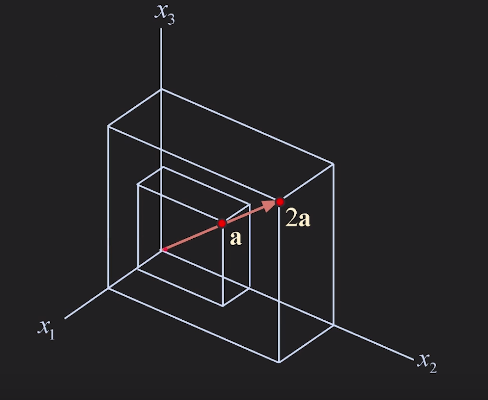
vectors in R^3
a = [[1], [5], [4]]
백터들의 대수학적 성질들

벡터 간에는 합의 법칙이 적용된다.
-덧셈 간의 교환 법칙, 결합 법칙, 항등원이 성립
백터와 스칼라 간에는 곱의 법칙이 적용된다.
- 벡터 스칼라의 분배 법칙, 교환 법칙, 벡터 곱하기 1은 벡터 그 자신이라 1은 벡터 스칼라 곱의 항등원이다.
- linear combination: vector equation
R^n space에서 v1, v2,.., vn의 합을 linear combination이라 부른다.
벡터에 곱해진 c는 scalar이며 벡터의 weight라 한다. (가중치)

- can b be generated as a linear combination of a1 and a2?
a1=[[1], [-2], [-5]]
a2=[[2], [5], [6]]
b=[[7], [4], [-3]]
x1 a 1 + x 2 a 2 = b
x1*[[1], [-2], [-5]] + x2*[[2], [5], [6]] = [[7], [4], [-3]]
결국 벡터 b와 a1, a2 linear combination generated는 augumented matrix와 같다

해당 벡터들을 column으로 두는 augmented matrix가 있는지를 묻는 것과 같다.
vector equation solution set== augmented matrix solution set
- Span {}
Span {v1,..., vp}
is the collection of all vectors that can be written in the form
c1 v1 + c2 v2 +...+ cpvp

vector b in Span {v1,..., vp},
vector equation have a solution,
augmented matrix have a solution,
세 개는 같은 질문이다.
Span을 씀으로써 augmented matrix가 해를 지니는지를 더 짧게 표현할 수 있다.


