2.5 Matrix Factorization

- Factorization(인수분해)
a product of two or more matrices
하나의 matrix를 2개 이상의 matrix를 표현하는 것을 Factorization이라고 한다.
- LU Factorization

L: unit lower triangular matrix(하삼각행렬)
U: echelon form
아래 예시에서는 A를 LU Factorization을 만들기 위해 row interchange, scaling 없이
row replacement 연산만을 통해 L(unit lower triangular maxtrix)을 만든다.

A,b,L,U 가 주어져있을때의 연산이다.
1. A= LU
A matrix를 LU형태로 만들고자 한다.
U는 row replacement operation만을 통해 만든 echelon form이다!
A를 L,U의 곱으로 표현할 수 있다.

2. Ax = b
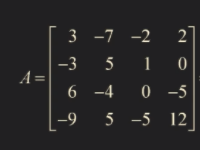
3. LUx = b Ux = y

L과 b를 augmented matrix로 만든다.
L,b 의 augmented matrix를 row reduction을 통해 reducted echelon form으로 만든다.
4. Ly = b
Ux = y
backward phase와 같다.

- LU Factorization Algorithm *only by row replacement

diagonal은 모두 1이다.
왜냐하면 forward phase의 row reduction만 하고 있다
애초에 elementary matrix는 identity matrix에서 1번의 row operation,
그중에 scaling, interchange가 아니라 row replacement를 한 형태이기 때문이다.
그렇기에 가운데 대각선(diagonal)의 값들은 그대로 1이 유지된다.

unit lower triangular elementary matrices

unit lower triangular
invertible 한 것들의 multiple또한 invertible하다.
elemenatary matrix는 invertible하다
즉, (E_p .. E_1)이 invertible하다
그러므로 (E_p .. E_1)^(-1)이 가능하다.
그래서,
(E_p .. E_1)A = U 양변에 (E_p .. E_1)^(-1)을 곱하면
(E_p .. E_1)(E_p .. E_1)^(-1)A = (E_p .. E_1)^(-1)U
*(E_p .. E_1)(E_p .. E_1)^(-1) = I
A = (E_p .. E_1)^(-1)U가 된다.
L은 unit lower triangular 즉, (E_p .. E_1)으로 표현가능하다.
unit lower triangular의 inverse 역시 unit lower triangular이다

A를 L(unit lower trianlgular matrix)로 만드는 법
1. A를 echelon form으로 reduction하는 것이 가능하다면
그 과정은 row replacement opeartions이다.
2. L(unit lower trianlgular matrix) 속의 entries은
L을 I로 row operation을 통해 reduced하는 과정에 있는 것과 같다.
A를 echelon form으로 reduction
그 과정에서 각각의 elemenatary matrix가 주어졌고 inverse를 알고 있다.
Identity matrix의 inverse를 계속 취해준다.

LU factorization 만들기
LU factorizatio으로 만들고 A = LU인지 확인
- Example2
처음에 A를 echelon form U로 만든다.

echelon form에 맞게 leading entry(pivot position)를 만든다.

이었으므로
A를 U로 만드는 과정에서 각 column을 pivot position의 역연산 한 것으로 diagonal matrix 밑에 부분을 채워나간다.
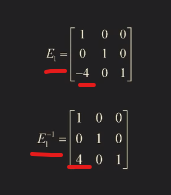
E_1 => E_1^(-1)


L을 Elementary matrix 곱의 역연산을 곱한 것으로 표현하므로 그렇다.
Row reduction 했던 것을 거꾸로 만드는게 복잡하므로 더 간단한 방법이 있다.
piviot position을 1로 만드는게 핵심이다.
pivot postion 밑에 entry들을 pivot을 1로 만드는 scaling에 같이 포함시켜 scaling한다.
pivot position 밑에 entry들만 같이 scaling 연산하는 이유는
L 즉, unit lower triangular matrix를 만드는 것이기 때문.

- General Case
PA = LU
p는 permutations matrix
row opearation interchange 적용

3번째 row equvalent한 matrix에서 2번째 row,와 3번째 row를 interchange한다.
- Numerical Notes
1. LU ~ (2n^3)/3 flops
square matrix가 주어졌을 때
LU factorization하는데 (2n^3)/3 flops(사칙연산) 가량의 컴퓨터 연산이 들어간다.
2. A^(-1) ~ 2n^3
inverse에는 2n^3이 소요된다.
3. Ly =b, Ux = y ~ 2n^2
2n^2 소요
4. A^(-1)b ~ 2n^2
2n^2소요
5. If A is sparse(entry 대부분이 0인, 희소행렬), then L and U may be sparse, too,
whereas is A^(-1) likely ro be dense
핵심은 matrix A가 sparse일때 L,U도 대부분 Sparse하다.
하지만 A^(-1)은 dense하기 쉽다.

A^(-1)의 경우 n^2 메모리를 차지
하지만 LU를 사용하면 예제의 경우 3줄 이런식으로 저장할 수 있다.
메모리 측면에서 이점이 있다.
0인 부분은 저장하지 않는다.
또한 0이 부분은 스킵하므로 연산속도도 빨라진다.
LU 사용시 메모리의 이점, 연산속도의 이점이 있기에 A를 LU로 변환하여 문제를 해결한다.
'Math > Linear algebra' 카테고리의 다른 글
| [인프런|2.6] Matrix Algebra | Subspaces of Rn (0) | 2020.12.30 |
|---|---|
| [인프런|2.4] Matrix Algebra | Partitioned Matrices (0) | 2020.12.22 |
| [인프런|2.3] Matrix Algebra | Characterizations of Invertible Matrices (0) | 2020.12.22 |
| [인프런|2.2] Matrix Algebra | The inverse of a Matrix (0) | 2020.12.20 |
| [인프런|2.1] Matrix Algebra | Matrix Operations (0) | 2020.12.19 |



