[인프런|Dynamic Programming(1)] 영리한 프로그래밍을 위한 알고리즘 강좌

Dynamic Programming

 

Recursive의 경우 이미 했던 호출을 다시 부르는 중복이 발생하여 효율이 떨어진다.

ex) Fibonacci Numbers

Memoization(Top-down)

배열에 중간 계산 결과를 저장한다(caching)

시작이 상위 사례부터 하위 사례(base case)까지 점점 작아지면서 호출되므로

위에서부터 시작된다하여 Top-down이라 한다.

 

 

Dynamic programming(Bottom-up)

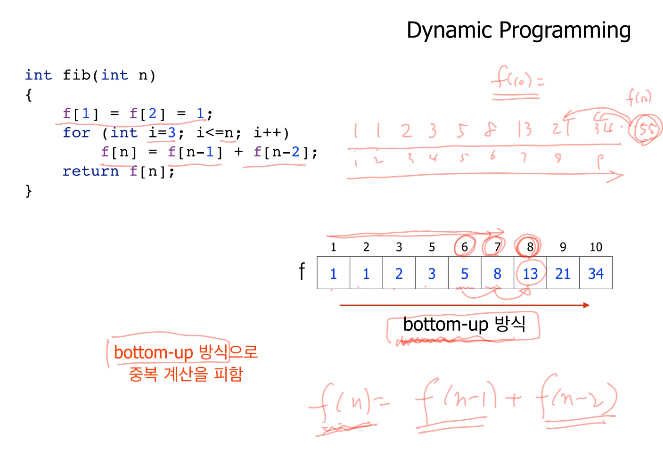
초기 작은 case부터 상위, 최종 case까지 값을 계산하면서 올라온다하여

Bottom-up이라 한다.

 

 

binomial coefficient 이항계수 계산

N개 중에 K를 뽑는 경우를 계산한다.

수학적으로는 N! / (N-K)! K! 과 같이 풀 수도 있겠지만

컴퓨터 상에서 그렇게 풀려고하면 비효율적이다 

100개 중 98개를 뽑는 경우 100! / 98! 
일일 계산 되기 때문에 그러면 서로 약분이 되게 하더라도 그러한 루틴이 들어가야하며 그 과정도 복잡한 편이다.

역시 이 경우 또한 Recursive 이용할 때 피보나치 수열처럼 중복되는 경우가 발생한다.

점화식으로 푸는 방법은 (작은 사례로 쪼개서 문제를 해결할 수 있다)

N개 중에서 K개를 뽑는 경우를 

N개의 집합 중 'a'라는 원소를 뽑는 경우와 뽑지 않는 경우 2가지로 나누어서 생각해 볼 수 있다.

'a'라는 원소를 뽑아서 K개에 포함시키는 경우   N-1 개 중 K-1개를 뽑는 것과 같다 (이미 a가 포함되었으므로 K-1, N-1)

'a'를 K개에 포함시키지 않는 경우 N-1개 중에서 K개를 뽑는 것과 같다. (a를 N개에서 뺐으니 N-1이며 K개에 포함되지 않으니 나머지 원소들 중에서 K개를 뽑기 때문이다.)

작은 사례로 쪼갤 수 있으므로 Memoization, Dynamic programming으로 해결 가능하다.

 

Recursive로 풀때 중요한 점

- Recursive가 무한 루프에 빠지지 않도록 Base case가 있어야 한다. 

- Recursive가 Base case에 도달 가능해야한다.

 

Memoization case

int binomial ( int n, int k)

{

  if ( n ==k || k == 0)

    return 1;

  else if (binom[n][k] > -1 ) // 배열 binom은 -1로 초기화 되었다고 가정

    return binom[n][k];

  else {

    binom[n][k] = binomial(n-1, k) + binomial(n-1, k-1);

    return binom[n][k];

  }

}

 

 

Dynamic Programming case

 

int binomial( int n, int k)

{

  for (int i = 0; i<=n ; i++) {

    for ( int j=0; j<=k && j<=i; j++) {

      if (k==0 || n == k)

        binom[i][j] = 1;

      else

        binom[i][j] = binom[i-1][j-1] + binom[i-1][j];

    }

  }

  return binom[n][k];

}

 

 

Memoization vs Dynamic programming
- 순환식의 값을 계산하는 기법

- 둘 다 동적게획법의 일종이다

- Memoization Top-down 방식, 실제 필요한 subproblem만을 푼다.

Dynamic Programming은 Bottom-up방식, recursion에 수반되는 overhead가 없다.